Turn, turn, turn, turn
UPDATED. Four rotations of 90° and you get back to where you started .... always?
Verlag: Texas Instruments UK
Herausgeber: Barrie Galpin
Fach: Mathematik
Schlagwörter Transformationen
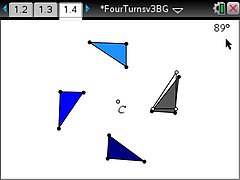
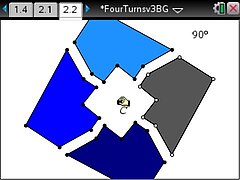
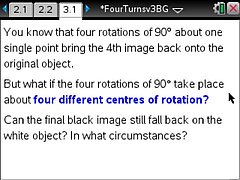
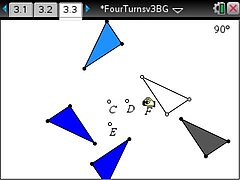
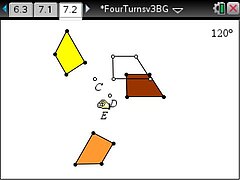
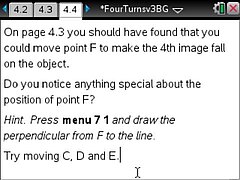
We know that when you repeatedly rotate an object by an angle of 90°, after four rotations the final image comes back to lie on the original object??if the same centre of rotation is used each time. But is that true if and only if the same centre of rotation is used? In other words is it possible for the four rotations to have different centres and the final image still to be coincident with the original object? If it is possible, then how are the four centres of rotation related? TI-Nspire provides an ideal tool to carry out this investigation.
The TI-Nspire document FourTurns.tns provides a guided investigation into the effect of four rotations of 90°, both about the same point and about four different points.
For younger students who are meeting mathematical rotation for the first time, it may be enough to consider only rotation about a single point. This can be done using just the first two problems of the document.
Alternatively you may prefer students to start with a blank document and experience the delight of producing the rotations themselves, in which case full detailed instructions and key presses are provided.