Pythagoras' Theorem

Discover, confirm, illustrate and use Pythagoras' Theorem
Publisher: Texas Instruments UK
Editor: Barrie Galpin
Author: Jay Timotheus
Topic: Mathematik
Tags Pythagoras
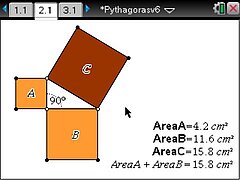
The first problem in the TI-Nspire document offers students a non-right-angled triangle with squares drawn on each side. As they change the shape of the triangle they realise that only when it is right-angled does the sum of the areas of the squares on the two shorter sides equal the area of the square on the longest side. The next step is to move the corners of a triangle that has been constructed so that it remains right angled - so confirming (but not proving!) the validity of the theorem.
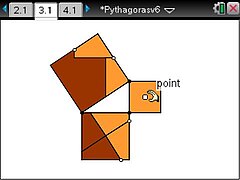
In problem 3 a famous dissection is used to further illustrate the theorem??students can drag parts of the smaller squares and see that they fit onto the largest one. (See screenshot above.)
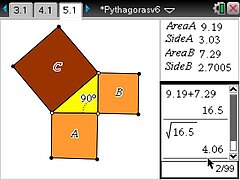
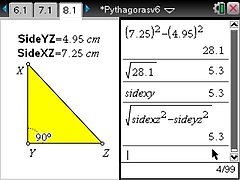
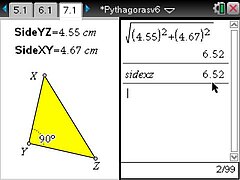
Students go on to calculate missing areas and then missing side lengths of right-angled triangles. A feature of the activity is that every student can draw a different triangle, carry out the calculations and then check the answers.
This activity includes a 3-page handout that guides students through eight problems in a TI-Nspire document. Together these provide all the technical help they will need.
This activity forms part of the OxBox, published by Oxford University Press to support their course 'Oxford GCSE Maths'. http://www.oup.com/oxed/secondary/2010gcse/