TI-Nspire CAS in Engineering Mathematics: Parametric Equations for a Great Circle
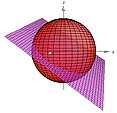
Find parametric equations for curve of intersection, e.g. sphere and plane
Publisher: T³ Europe
Author: Michel Beaudin, T³ Europe
Topic: MINT
Tags
In single variable calculus, students usually find point(s) of intersection of two curves y=f(x) and y=g(x) by solving an equation f(x)=g(x). When they move to multivariable calculus, students are rarely asked to find parametric equations for the curve of intersection of 2 surfaces - the exception being when both surfaces are planes! In the general case, a surface may be described by z=f(x,y) or more probably by an equation of the form f(x,y,z)=0. They don't really know how to attack the system of two equations in three unknowns.
We will be finding parametric equations for the curve of intersection of a sphere and a plane passing through the center of the sphere, which is a great circle (a circle having the same radius as the one of the sphere). The problem will be solved using three different approaches:
- We will find parametric equations by simply using the "solve system" command. But we will need two sets of parametric equations (one for each "half-circle") and this will produce a non satisfactory graph.
- My favorite one: after a substitution and a completion of the square, the first trigonometry identity will be used and a single set of parametric equations will be obtained.
- And the third one will be related to a system of first order ODEs originating from the cross product of the gradient vectors.
