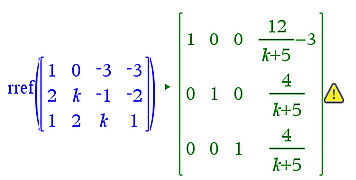TI-Nspire CAS in Engineering Mathematics

Using TI-Nspire CAS for teaching and learning of mathematics in engineering courses such as calculus (single variable, multiple variables), linear algebra, differential equations, complex analysis …
Publisher: T³ Europe
Author: Michel Beaudin, T³ Europe
Topic: MINT
The examples in this section give ideas of the value and possibilities of using TI-Nspire CAS for teaching, learning and better understanding mathematics in engineering courses such as calculus (single variable, multiple variables), linear algebra, differential equations, complex analysis …
For each topic we tried to solve the problems as follows in original, creative, innovative ways:
- A solution is shown using two different approaches. This is rarely seen in textbooks and sometimes impossible to achieve without a CAS. Moreover, using two different methods requires doing more and not less mathematics: this is one of the most important benefit of CAS and, unfortunately, it has not been exploited enough.
- We present solutions that also involve comments on some specific built-in TI-Nspire CAS functions. Teaching mathematics with TI-Nspire CAS can become a very enthusiastic experience because we don’t need to use complicated commands to solve a problem.
- Some problems could have been solved without TI-Nspire. But the avaibility of graphs, tables, animations, … gives a new taste to the solution. And for the other problems, a CAS is necessary because some heavy computations would have been too long to do by hand, if not impossible.
- We are advocates of "a computer algebra point of view": if pens and paper techniques are usually used to solve a specific problem, make the use of CAS acceptable with a solution involving more details than before. Both ways ─ those who prefer the pens and paper approach and those who are pushing for use of CAS ─ will be served and, at the end, students will have deepened their understanding of mathematics.
Some Examples:
- System of Three Linear Equations in Three Variables
- Parameter in a System of Linear Equations
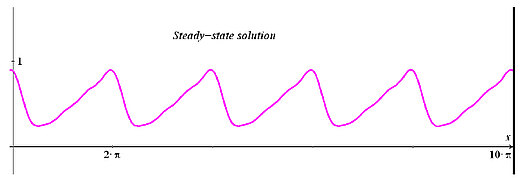
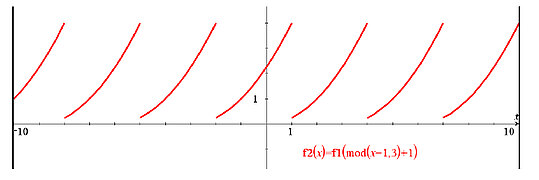
- Using Fourier Series to Find the Steady-State Solution
- Line Integral: Residue Integration and Laurent Series
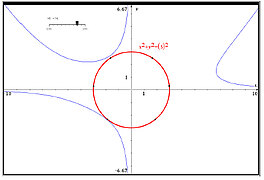
- Highest Temperature in a Disk
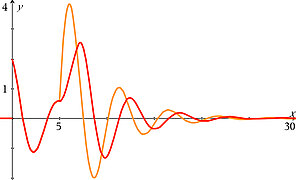
- Falling Object Under Air Force Resistance
- Geometric Transformations and Matrices
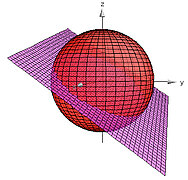
- Parametric Equations for a Great Circle
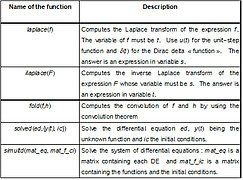
- Library of Laplace Transforms
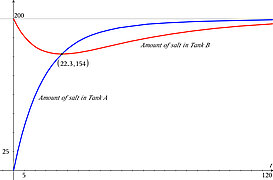
- Unit Step and Impulse - Spring-Mass Problems
- First Order Systems and Symbolic Matrix Exponentiation
Technical Remarks
These files were created using TI-Nspire CAS on the computer view. Of course they can can be used on the handheld (some computations might be longer). Also, " Notes " pages are inserted into our files in order to be able to introduce the problem using mathematical notations and give some mathematical background. For instance, here are the math boxes' attributes chosen in each document:
- A black math box has no simplification, it is used only for writing mathematical expression.
- A blue math box is used to define a mathematical object or to perform a mathematical operation with the attribute of hiding output. Clicking on the box displays the output in green.
Before opening a file, please set the Real and Complex Format to Rectangular in the Document Settings of TI-Nspire CAS. All other settings should be the default ones of Nspire CAS. If you have any questions, remarks or suggestions, please feel free to email Michel Beaudin.